PSpice war anfangs nichts weiter als die auf einem PC lauffähige Version des Simulators Spice. Im Anschluss an die Pspice-Version 1 gab es regelmäßig Neuerungen, die den Funktionsum- fang des Programms erweiterten. Drei dieser Erweiterungen waren m.E. von ganz besonderer Bedeutung: Die Einführung einer graphischen Anzeigemöglichkeit für die Simulations- ergebnisse (PROBE), die Einführung der Möglichkeit zur graphischen Eingabe von Schaltplan und Simulationsanweisungen mithilfe eines Schaltplaneditors (SCHEMATICS, später CAPTURE) und ab der PSpice-Version 4 die auch für normale Nutzer relativ einfach anwendbare Möglichkeit, selbstständig PSpice-Modelle zu erstellen: Analog Behavior Modeling (ABM). Darum geht es in diesem Abschnitt.

Den Kern von ABM bilden gesteuerte Spannungs- und Stromquellen. Steuervariablen dieser Quellen sind (u.a.) Ströme und Spannungen an verschiedenen Stellen des Schaltkreises. Auf die Steuervariablen dürfen bestimmte mathematische Operatoren und Funktionen angewendet werden. Als Ergebnis ergibt sich der Ausgangsstrom, bzw. die Ausgangsspannung der gesteuerten Quelle.

Anwendungsbeispiele zur Einführung in die Arbeit mit ABM

Beispiel 1: Invertierender Verstärker mit der Verstärkung 10

Für dieses Beispiel wird die gesteuerte Spannungsquelle EVALUE aus der Bibliothek abm.olb verwendet. Bild 1 zeigt die Schaltung. Zur Bezeichnung der Potentiale der Pins gesteuerter Quellen wird der Pinname mit einem vorangestellten %-Zeichen verwendet. Das Potential am Pin IN+ heißt folglich v(%IN+). Dieses Potential muss mit dem Faktor -10 multipliziert werden, damit die Verstärkung 10 und das gewünschte invertierende Verhalten erreicht wird. Nach Doppelklick auf das Schaltzeichen öffnet sich der Property-Editor und man kann in die Zeile EXPR den Ausdruck zur Berechnung der Ausgangsspannung eingeben. Dazu müssen Sie den dort bereits vorhandenen Eintrag überschreiben mit: v(%IN+)*(-10). Bild 2 zeigt das korrekt ausgefüllte Fenster des Property-Editors:

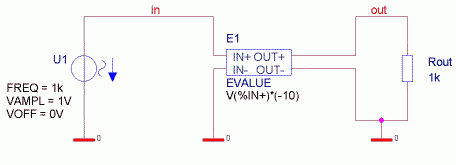
Bild 1: Invertierender Verstärker mit A = 10, realisiert mit einer gesteuerten Quelle EVALUE

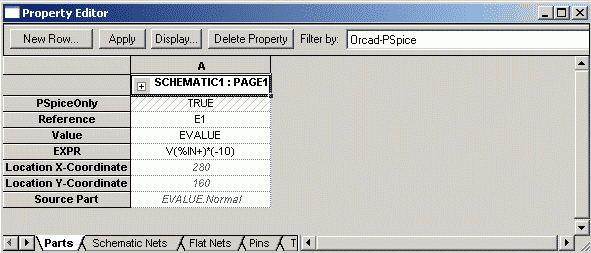
Bild 2: Property-Editor der gesteuerten Quelle EVALUE. Bei EXPR ist der erforderliche Wert eingetragen

Bild 3 zeigt das gewünschte Ergebnis:

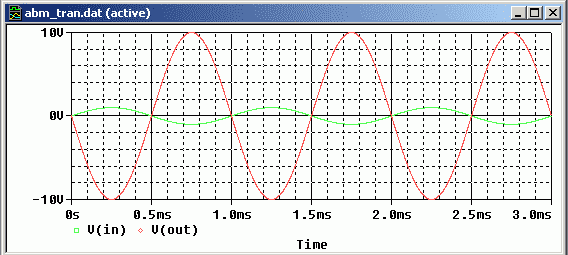
Bild 3: Probefenster nach Simulation der Schaltung von Bild 1

In ABM erlaubte SteuervariablenSyntax

Potentiale (bezogen auf 0 (AGND)

v(Kotenname)
Spannungen zwischen zwei Knoten

v(Knotenname1,Knotenname2)
Ströme durch unabhängige Spannungsquellen (z.B. VDC)

i(Quellenname)
Ströme durch Induktivitäten

i(Name der Induktivität)
Parameter

i(Name des Parameters)
Aktueller Simulationszeitpunkt

time
Schaltungstemperatur

temp
Laplace-Variable

s

In Beispiel 1 haben Sie bereits einen in ABM zulässigen Operator kennen gelernt: Den Operator * zu Ausführung von Multiplikationen. Es gibt für ABM darüber hinaus noch mehr als 40 weitere zulässige Operatoren und Funktionen. Eine Zusammenstellung sämtlicher in ABM erlaubter Operatoren und Funktionen finden Sie hier: ABM-Operatoren und -Funktionen.

Beispiel 2: Modellierung einer B2-Gleichrichterbrücke

Bild 4 zeigt eine Schaltung zur Erzeugung der Ausgangsspannung eines B2-Gleichrichters für eine gegebene Eingangsspannung:

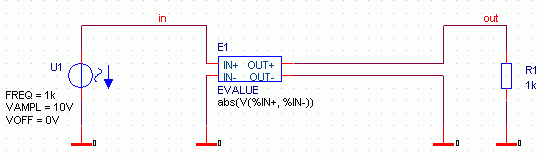
Bild 4: Mit ABM modellierter Gleichrichter B2

Bild 5 zeigt das Fenster des Property-Editors von EVALUE. Bei EXPR ist der erforderliche Ausdruck abs(v(%IN+,%IN-))bereits eingetragen. Bei der Erzeugung dieses Ausdrucks wurde erstmalig die Funktion ABS(x) verwendet. Die verwendete Syntax der Eingangsspannung (mit dem Komma als Differenzbildner) wurde in der Tabelle weiter oben beschrieben.

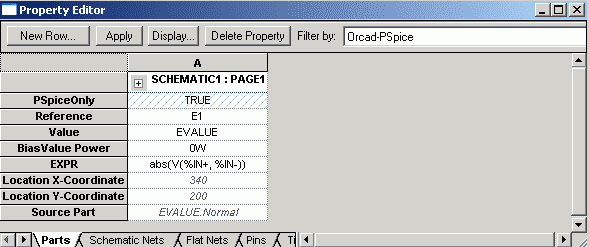
Bild 5: Property-Editor von EVALUE mit Eintrag zur Modellierung eines B2-Gleichrichters

Bild 6 zeigt die erwartete Ausgangsspannung des B2-Gleichrichters:

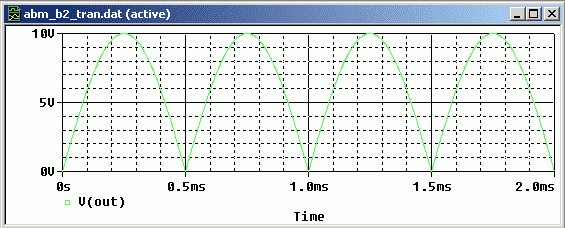
Bild 6: Ausgangsspannung des B2-Gleichrichters

Beispiel 3: Modellierung einer Einweg-Gleichrichterschaltung

Bild 7 zeigt eine Schaltung zur Erzeugung der Ausgangsspannung eines Einweg-Gleichrichters für eine gegebene Eingangsspannung:

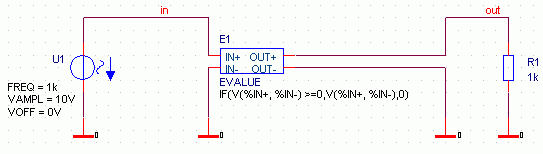
Bild 7: Mit ABM modellierter Einweg-Gleichrichter

Bild 8 zeigt das Fenster des Property-Editors von EVALUE. Bei EXPR ist der erforderliche Ausdruck IF(v(%IN+,%IN-)>=0,(v(%IN+,%IN-),0)bereits eingetragen. Bei der Erzeugung dieses Ausdrucks wurde erstmalig der Operator >= sowie die Funktion IF(t,x,y) verwendet.

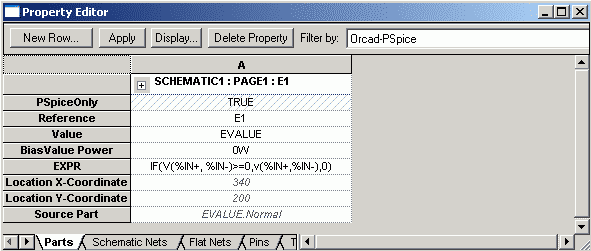
Bild 8: Property-Editor von EVALUE mit Eintrag zur Modellierung eines Einweg-Gleichrichters

Bild 9 zeigt die erwartete Ausgangsspannung des Einweg-Gleichrichters:

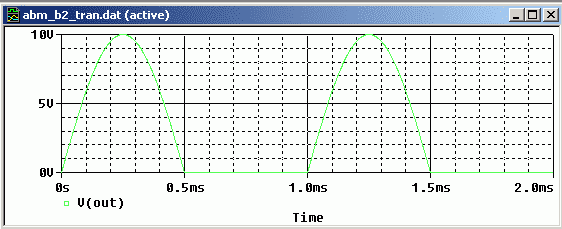
Bild 9: Ausgangsspannung des Einweg-Gleichrichters

Beispiel 4: Erzeugung einer Folge aus 3 Perioden einer Sinusschwingung mit 1 kHz

Dieses Beispiel dient dazu, die Wirkung der Funktion STP(x) zu erläutern. Es sollen damit aus einer Sinusschwingung 3 Perioden ausgeschnitten werden. Für die Ausgangsspannung v(out) soll gelten:

v(out)=0 für t<2ms
v(out)=sin(2*3.14*1k*time) für 2ms<t<5ms
v(out)=0 für t>5ms

Gewählt wird wieder eine gesteuerte Spannungsquelle EVALUE. Bei EXPR muss folgender Wert eingetragen werden: v(%IN+,%IN-)*STEP(time-2ms)*STEP(5ms-time). Die Schaltung zeigt Bild 10. Das Simulationsergebnis sehen Sie in Bild 11.

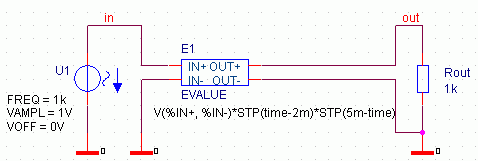
Bild 10: Schaltung zur Erzeugung eines Sinusausschnitts

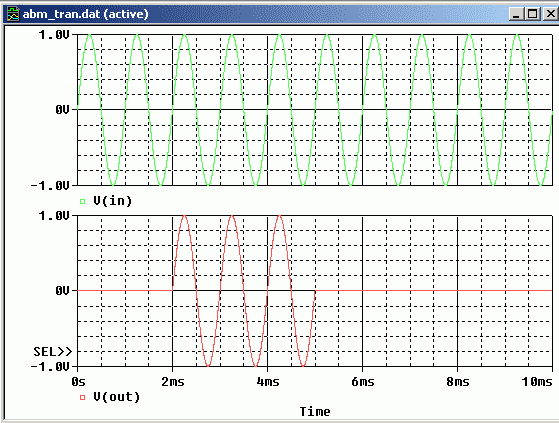
Bild 11: Simulationsergebnis mit dem gewünschten Sinusausschnitt

Die in ABM verfügbaren gesteuerten Quellen

Sie haben sich oben mit Hilfe von 4 Beispielen mit der Nutzung von ABM etwas vertraut gemacht. Dabei haben Sie immer die Quelle EVALUE verwendet, obwohl es insgesamt 8 verschiedene gesteuerte Quellen gibt. Das war kein Zufall, denn die Quelle EVALUE ist in ABM die bei weitem wichtigste Quelle. Alle gesteuerten Quellen gibt es sowohl als gesteuerte Spannungsquellen, als auch als gesteuerte Stromquellen. Die Namen der gesteuerten Spannungsquellen beginnen mit dem Buchstaben E, z.B. EVALUE. Die Namen der gesteuerten Stromquellen beginnen mit G. Die zu EVALUE analoge Stromquelle heißt GVALUE. In der folgenden Aufstellung werden nur die gesteuerten Spannungsquellen beschrieben, da die Handhabung der entsprechenden Stromquellen m.E. keine spezielle Beschreibung erfordert. Ein Anwendungsbeispiel für eine Quelle GVALUE finden Sie in Beispiel 5.

Zu den hier beschriebenen gesteuerten Quellen gibt es meistens auch noch mehrere Derivate. Manchmal lassen sich diese einfacher handhaben, manchmal stellen sie eine Brücke zu früheren Programmversionen her und haben heute kaum noch eine Bedeutung.

Es gibt (grundsätzlich) die folgenden gesteuerten Spannungsquellen:

Quelle	Bedeutung
EVALUE:	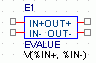Die Quelle liefert am Ausgang eine Spannung, die sich aus dem Eintrag bei EXPR ergibt, der im Property-Editor vorgenommen wurde. Erlaubt sind darin die in ABM zulässigen Steuervariablen sowie die zulässigen Operatoren und Funktionen
ETABLE:	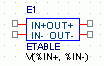Die Quelle besitzt zwei editierbare Attribute: EXPR und TABLE. TABLE beschreibt eine Wertetabelle aus Koordinaten- paaren. EXPR liefert, wie bei EVALUE, einen Ausdruck, dem über die Wertetabelle ein Wert für die Ausgangsspannung der Quelle zugeordnet wird. Zwischen den Punkten der Wertetabelle wird linear interpoliert. Ist der in EXPR berechnete Wert kleiner/größer als der kleinste/größte Wert von TABLE, dann wird dieser kleinste/größte Wert für die Ausgangsspannung verwendet. Ein Anwendungsbeispiel für ETABLE finden Sie in Beispiel 6.
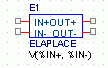
ELAPLACE: LAPLACE	Die Quelle besitzt zwei editierbare Attribute: EXPR und XFORM. XFORM beschreibt einen Laplace-Ausdruck (z.B. 1/s). EXPR liefert, wie bei EVALUE, einen Ausdruck, auf den die bei XFORM angegebene Laplacetransformation angewandt wird. Das Ergebnis der Transformation wird als Spannung an den Ausgang der Quelle geliefert. Nicht ganz so universell wie ELAPLACE, dafür aber sehr übersichtlich und für Anwendungen in der Regelungstechnik völlig ausreichend, ist der Baustein LAPLACE, der auf ELAPLACE beruht. Anwendungsbeispiele für den Baustein LAPLACE und weitere Hinweise zur Laplacetransformation mit PSpice finden Sie im Kapitel 3 von Regelungstechnik mit PSpice.
EFREQ:	Die Quelle besitzt in der Hauptsache zwei editierbare Attribute: EXPR und TABLE. TABLE beschreibt mit Hilfe einer Liste von Koordinatentripeln (Frequenz, Amplitude, Phase)oder wahlweise (Frequenz, Realteil, Imaginärteil) einen Filterfrequenzgang, der auf den bei EXPR definierten Vorgang angewandt wird.

Weitere Beispiele zur Einführung in die Arbeit mit ABM

Beispiel 5: Erstellen von Modellen für Bauteile, bei denen der Verlauf der der U/I-Kennlinien mathematisch mittels ABM-Operatoren und -Funktionen beschreibbar ist. Hier: Erzeugung des Modells eines spannungsabhängigen Widerstands (VDR)

Für einen VDR gilt: U = C ^. I^β mit U in Volt und I in Ampere. C ist eine Formkonstante, die festlegt, bei welcher Spannung der Strom gerade 1 A beträgt. Im vorliegenden Beispiel sei C = 100. β ist eine Materialkonstante. Für das vorliegende Beispiel sei β = 0,2.
Aufgelöst nach I ergibt das: I = (U/100)⁵. Bild 12 zeigt eine Schaltung zur Realisierung dieses Ausdrucks. Es wird hier erstmalig eine gesteuerte Stromquelle GVALUE verwendet, außerdem die Funktion PWRS:

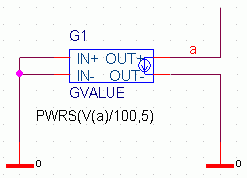
Bild 12: Schaltung zur Erzeugung des Modells für einen VDR

Bild 13 zeigt eine Testschaltung, mit der mittels DC-Sweep von U1 die I/U-Kennlinie überprüft werden kann.:

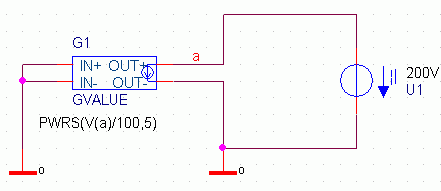
Bild 13: Testschaltung zur Erzeugung der Kennlinie des oben realisierten Modells eines VDR

Bild 14 zeigt das zufriedenstellende Ergebnis:

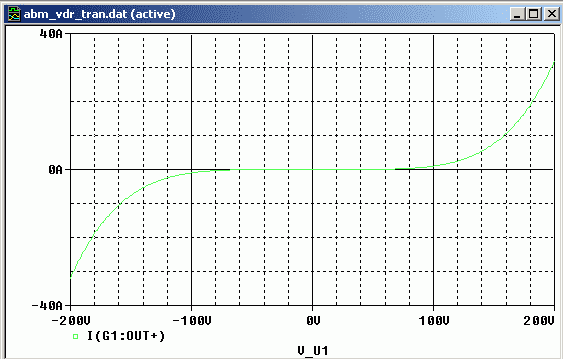
Bild 14: Kennlinie des modellierten VDR

Beispiel 5: Modell eines Operationsverstärkers mit einem Verstärkungsfaktor A = 10⁶ und einer Versorgungsspannung von +15V.

Bild 15 zeigt eine geeignete Schaltung unter Verwendung einer Quelle ETABLE. ETABLE ist so eingestellt, dass der bei EXPR berechnete Wert an den Ausgang weitergegeben wird. Allerdings: Nur bis +15V. Größere Werte werden beschnitten.

Bild 16 zeigt die Ein- und Ausgangsspannung für u_in = 10 μV. Bild 17 zeigt die gleichen Spannungen für u_in = 20 μV.

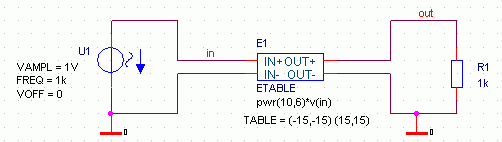
Bild 15: Operationsverstärker, modelliert mit ABM

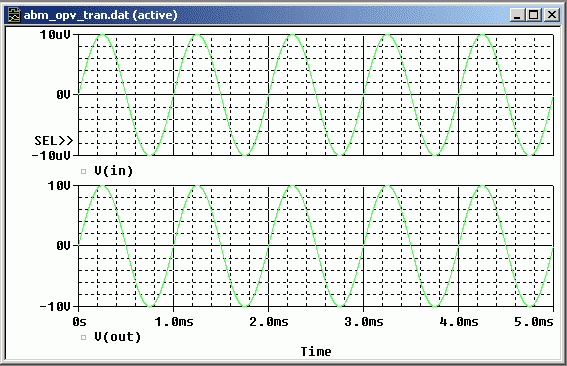
Bild 16: Ein- und Ausgangsspannung des OPV. u_in = 10uV

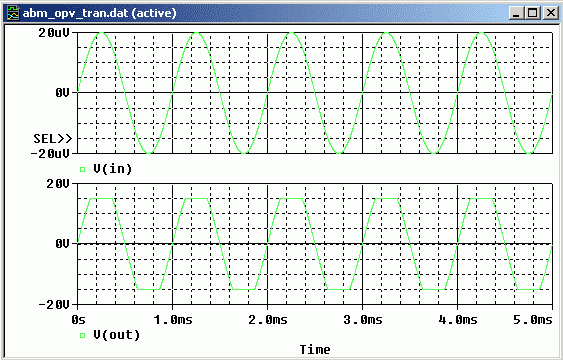
Bild 17: Ein- und Ausgangsspannung des OPV. u_in = 20uV

Bild 18 zeigt die Beschaltung des oben modellierten OPV als invertierender Verstärker mit der Verstärkung 10. Bild 18 zeigt das (korrekte) Simulationsergebnis.

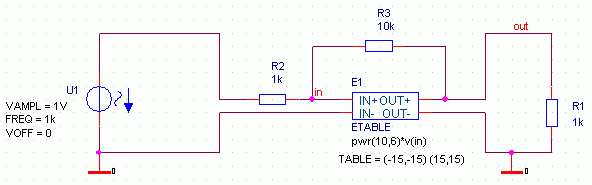
Bild 17: ABM-OPV, beschaltet als invertierender Verstärker

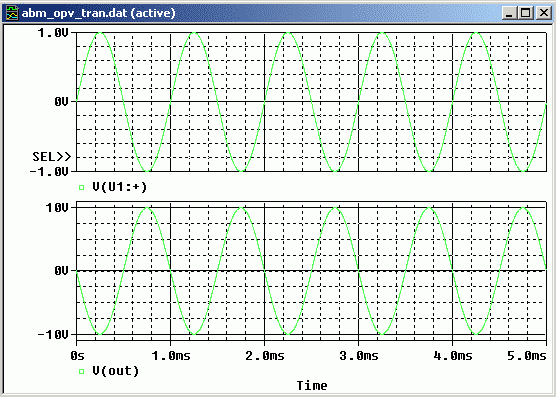
Bild 18: Ein- und Ausgangsspannung des invertierenden Verstärkers von Bild 17