|
|
|

|
 Robert Heinemanns PSPICE-Seiten |
|
Beispiel Fi5:
Über die Simulation digitaler Filter mit PSpice |
Aufbau digitaler Filter
Bild 1 zeigt den prinzipiellen Aufbau einer Schaltung zur Simulation digitaler Filter. Sie besteht aus diversen Addierern (die
mit dem Plus-Zeichen im Kreis), Multiplizierern (die mit dem X im Kreis) und Totzeitgliedern (TD in
eckiger Kiste):
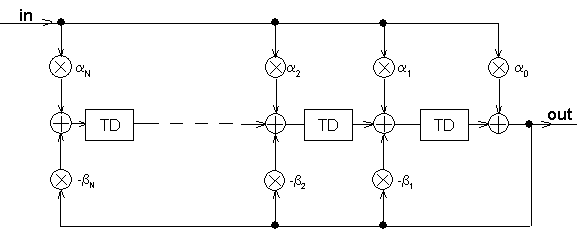
Bild 1: Grundsätzlicher Aufbau einer Schaltung zur Simulation digitaler Filter. Die Schaltung besteht
aus Addierern, Multiplizierern und Totzeitgliedern
Alle in Bild 1 vorhandenen Bauteile sind in PSpice vorhanden und der Simulation digitaler Filter steht
folglich nichts im Wege. Die PSpice-Addierer heißen SUM und befinden sich in der Bibliothek ABM. Die
Multiplizierer heißen MULT. Auch die MULT-Glieder befinden sich in der Bibliothek ABM. Totzeitglieder lassen sich mit Hilfe
des ABM-Bauteils LAPLACE realisieren. Kenntnisse von Laplace- und z-Transformation sind zum tieferen Verständnis
der Arbeitsweise digitaler Filter erforderlich, für den reinen Entwurf und die Anwendung digitaler Filter kommt
man aber, wie im Folgenden gezeigt wird, auch ohne Laplace- und z-Transformation gut zurecht, unverzichtbar allerdings sind Kenntnisse
grundsätzlicher Eigenschaften digitaler Filter, wie sie z.B. im Digitalfilter-Kapitel von Tietze/Schenk
vermittelt werden.
Man unterscheidet zwei grundsätzliche Formen digitaler Filter:
FIR-Filter werden so entworfen, dass darin keine Rückkopplungen der Ausgangsspannung verwendet werden. Dazu
werden sämtliche Koeffizienten βi gleich Null gesetzt. FIR-Filter
nutzen folglich nur die Koeffizienten αi.
IIR-Filter verwenden in der Regel sämtliche Koeffizenten der Schaltung von Bild 1, d.h. neben den αi
existieren auch die βi.
Im Folgenden wird in vier Schritten der Entwurf eines IIR-Filters gezeigt werden.
PSpice-gestützer Entwurf eines digitalen IIR-Hochpasses 3. Ordnung mit Butterworth-Abstimmung.
1. Schritt. Prinzipschaltung des Filters:
Aus der Theorie digitaler Filter weiß man, dass für das geplante Filter ein IIR-Filter 3. Ordnung erforderlich ist.
Bild 2 zeigt den prinzipiellen Aufbau. Die Filter-Koeffizienten werden mit Hilfe des Bausteins CONST aus
der Bibliothek ABM eingegeben. Zur Realisierung der Totzeitglieder wurden drei LAPLACE-Elemente platziert.
In Bild 2 stehen alle Koeffizienten noch auf ihren Defaultwerten (1). Sie müssen noch passend berechnet
werden. Auch die LAPLACE-Glieder enthalten noch ihren Defaultausdruck (1/1+s).
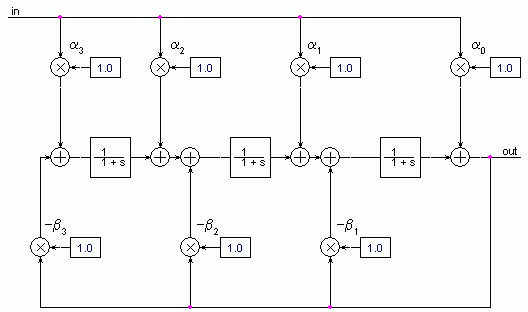
Bild 2: PSpice-gestützer Entwurf eines digitalen IIR-Hochpasses 3. Ordnung mit
Butterworth-Abstimmung: Prinzipschaltung.
2. Schritt. Wahl der Abtastfrequenz und Dimensionierung der Totzeitglieder:
Für dieses Beispiel wird als Abtastfrequenz fa = 10 kHz gewählt. Damit erhält man ein Filter, das nach
dem Abtast-Theorem bis 5 kHz (halbe Abtastfrequenz) brauchbar ist. Aus fa = 10 kHz berechnet sich die
Totzeit der drei Totzeitglieder zu TD = 1/fa = 0,1 ms. Einer Tabelle der Laplace-Transformationen kann man für ein Totzeitglied
den Ausdruck 1 / esTD entnehmen. Bild 3 zeigt die Schaltung mit korrekt dimensionierten
Totzeitgliedern:
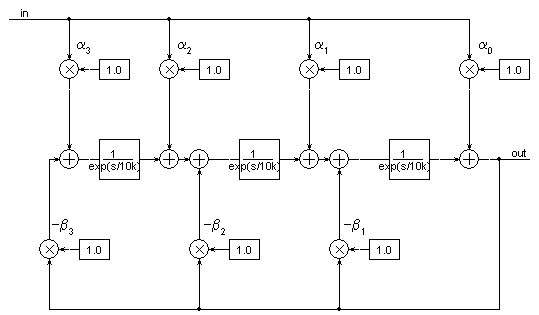
Bild 3: PSpice-gestützer Entwurf eines digitalen IIR-Hochpasses 3. Ordnung mit Butterworth-Abstimmung.
Die Totzeitglieder sind dimensioniert.
3. Schritt. Bestimmung der Filterkoeffizienten:
Beim Entwurf von Analog-Filtern nutzt man geeignete Computerprogramme zur Berechnung der frequenzbestimmenden
Bauteile. Auch zur Berechnung der Filterkoeffizienten digitaler Filter gibt es geeignete Software-Hilfen. Unter
http://www-users.cs.york.ac.uk/~fisher/mkfilter/trad.html
finden Sie Tony Fishers Programm zur Berechnung der Koeffizienten von IIR-Filtern. Tony Fishers Programm
liefert für den zu entwerfenden Butterworth-Hochpass ein Ergebniss, das auszugsweise in Bild 4 dargestellt ist. Die roten Teile
des Bildes sind von mir hinzugefügt worden. Sie verdeutlichen die Bestimmung der Filter-Koeffizienten aus den Angaben der
Abteilung RESULTS von Fishers Ergebnisausdruck:

Bild 4: Entwurf eines digitalen IIR-Hochpasses 3. Ordnung mit Butterworth-Abstimmung. Bestimmung der
Koeffizienten mit Tony Fischers IIR-Filterprogramm
Bild 5 zeigt das fertig dimensionierte Filter:
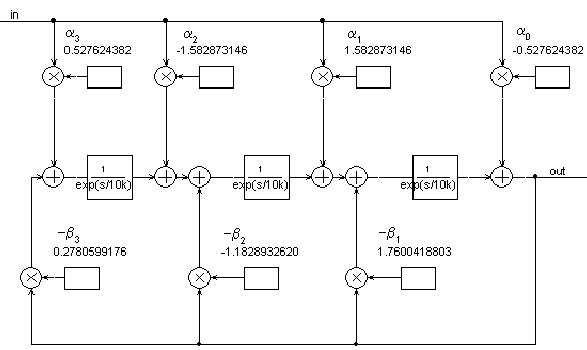
Bild 5: PSpice-gestützer Entwurf eines digitalen IIR-Hochpasses 3.
Ordnung mit Butterworth-Abstimmung. Fertiges Filter.
4. Schritt. Test des Filterentwurfs mit PSpice:
Bild 6 zeigt die Schaltung zur Aufnahme des Amplitudengangs, des Phasengangs und der Gruppenlaufzeit.
Die AC-Quelle am Eingang wird von 1 Hz bis 5 kHz (halbe Abtastfrequenz) mit 100 Punkten pro
Dekade gesweept. Bild 7 zeigt das Ergebnis der Simulation: Den Amplitudengang mit linarer y-Achse (oben) und in dB
formatierter y-Achse (darunter). Den Phasengang (hellblau) und die Gruppenlaufzeit (gelb).
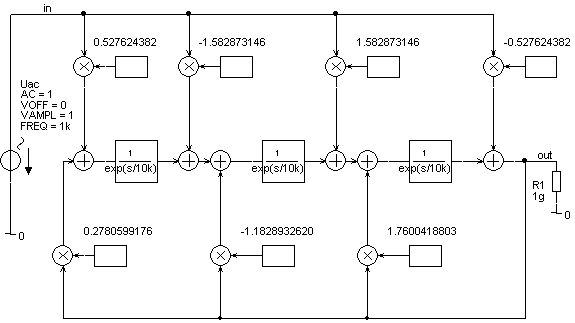
Bild 6: Digitaler IIR-Hochpass 3. Ordnung mit Butterworth-Abstimmung: Simulationsschaltung.
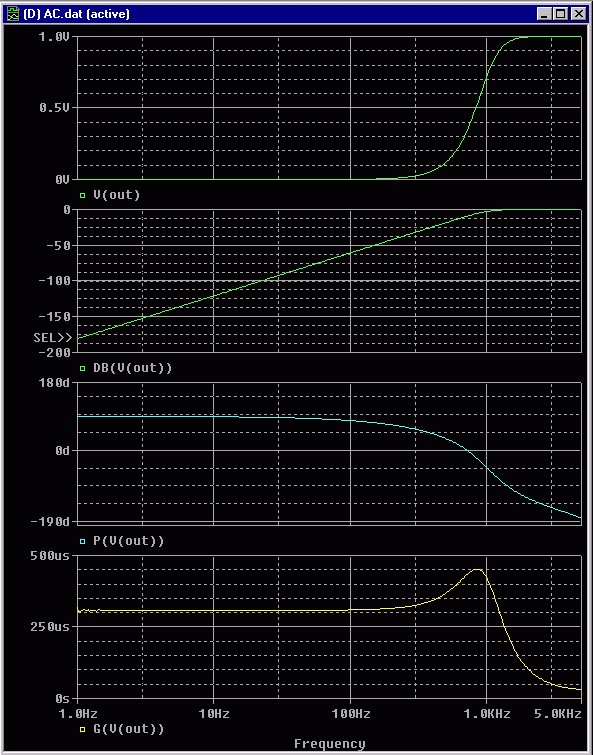
Bild 7: Digitales Filter von Bild 6: von oben nach unten: Amplitudengang linear,
Amplitudengang in dB, Phasengang und Gruppenlaufzeit
Bild 8 zeigt die Schaltung zur Aufnahme der zugehörigen Sprungantwort (Transient, Final Time = 8 ms,
Step Ceiling = 1u):
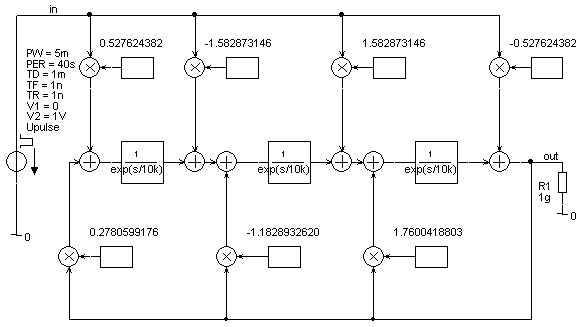
Bild 8: Digitales Filter von Bild 2: Schaltung zur Aufnahme der Sprungantwort
Bild 9 zeigt den Eingangssprung (oben) und die Sprungantwort (unten):
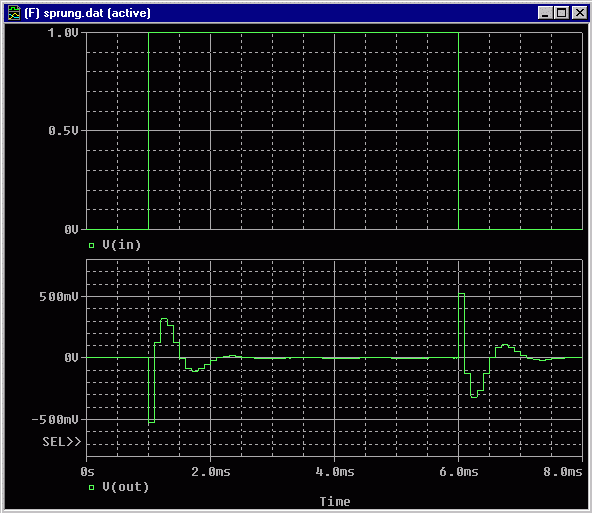
Bild 9: Digitales Filter von Bild 2: Sprungfunktion (oben) und Sprungantwort (unten)
Aus Bild 7 erkennt man, dass das Filter ein Hochpassfilter mit "maximal flachem" Frequenzgang
ist. Der Amplitudengang steigt unterhalb der Grenzfrequenz mit 60 dB/Dekade an. Die Grenzfrequenz liegt
bei 1 kHz. Aus Bild 9 erkennt man, dass das Filter ein Digitalfilter ist, dessen Totzeitglieder
jeweils 0,1 ms Totzeit bewirken. Also: Es handelt sich um einen digitalen Butterworth-Hochpass 3. Ordnung
mit einer Grenzfrequenz von 1 kHz und einer Abtastfrequenz von 10 kHz. Der Filterentwurf ist offensichtlich OK.
Download der Simulationsdateien zur Schaltung von Bild 6:
Falls Sie die Schaltung simulieren möchten, sich aber vor der Zeichenarbeit
scheuen, oder falls Sie mit dem Simulationssetup nicht
zurecht kommen, können Sie hier die Schaltung
mit fertigem Simulationssetup im SCHEMATICS- oder im CAPTURE-Format herunterladen.
Zur Simulation benötigen Sie die Euromodifikationen zu PSpice,
die Bestandteil meines Buches sind.
Damit Sie nach der Simulation automatisch die vorgefertigten Probe-Diagramme erhalten,
müssen Sie vor dem Start der Simulation in SCHEMATICS die Option
ANALYSIS/PROBE SETUP/RESTORE LAST PROBE SESSION wählen, bzw in CAPTURE im Fenster
SIMULATION SETTINGS die Option PROBE WINDOW/SHOW/LAST PLOT.
|
Für CAPTURE ab V10:
Laden Sie die unten angebotene selbstex- trahierende ZIP-Datei digifiltallgem_ cap.exe
herunter und starten Sie dann die Entpackung durch Doppelklick auf den Dateinamen.
Das Entpackprogramm schlägt Ihnen zum Aufbewahren der entpackten Dateien den Ordner
PSpice-Beispiele vor. Ein guter Vorschlag. Starten Sie anschließend aus CAPTURE
heraus digifiltallgem.opj:
Laden Sie hier digifiltallgem_cap.exe (39 kB)
|
|
Für SCHEMATICS:
Laden Sie die unten angebotene selbstex- trahierende ZIP-Datei digifiltallgem_ sch.exe herunter und starten Sie dann die
Entpackung durch Doppelklick auf den Dateinamen. Das Entpackprogramm schlägt Ihnen zum Aufbewahren
der entpackten Dateien den Ordner PSpice-Beispiele vor. Ein guter Vorschlag. Starten Sie anschließend aus SCHEMATICS
heraus digifiltallgem.sch:
Laden Sie hier digifiltallgem_sch.exe (29 kB)
|
Zurück nach: oben
|

|
|
